Chapter 1 - Risk factors
Risk factor epidemiology tries to separate the effects of the exposure being investigated from all other exposures. This is important because cancer may develop following a series of different exposures over a long period, so the identification of all possible exposures is challenging.
Establishing Causation
Study conditions in epidemiology are difficult to control, so a single study is rarely definitive, and evidence of causation depends on accumulated evidence. Interpretation of this evidence may be controversial.
Mobile phones and brain cancer
The INTERPHONE (INTERPHONE Study Group, 2010) and other large studies (Benson et al, 2013) have produced strong evidence that there is no association between mobile phone use and brain cancer, but controversy continues concerning a range of methodological issues (Lagorio and Röösli, 2014; Morgan et al, 2015).
The epidemiologist Bradford Hill (Hill, 1965) proposed certain aspects of a study which suggest causation.
Table 2: Bradford Hill’s Criteria for Causation
- Strength: An exposure which increases the risk of the outcome by 5% is less convincing than one which doubles it
- Consistency: Has the association been repeatedly observed in different places, circumstances and times?
- Specificity: Is the association limited to particular sites and types of disease?
- Temporality: Does the exposure precede the outcome?
- Biological gradient: Does the association show a dose–response curve?
- Plausibility: Is the causation biologically plausible?
- Coherence: This is related to plausibility – does the effect cohere with the generally known facts of the natural history and biology of the disease?
- Experiment: If some preventive action is taken, does it in fact prevent the outcome?
- Analogy: Has a similar exposure been shown to be associated with a similar outcome?
Study Design
Cancer risk factors are often suggested by observing variation in cancer incidence or mortality between populations differentiated by geography, time, occupation or other characteristics. Hypotheses developed from these observations are tested in analytical studies. These are typically cohort or case-control studies, but sometimes a randomised trial might be used.
Types of Epidemiological Study
Table 3: Advantages and Disadvantages of Different Study Types
Study type |
Advantages |
Disadvantages |
|---|---|---|
Cohort study |
Clear sequence of events Risk can be measured Low risk of selection bias |
Large numbers of participants needed with long follow-up period, so expensive and often slow New exposures difficult to addLoss to follow-up Change in exposure status during study Risk of confounding |
Randomised trial |
Clear sequence of events Risk can be measured Low risk of bias or confounding |
Large numbers of participants needed with long follow-up period, so expensive and often slow New exposures difficult to add Loss to follow-up Change in exposure status during study Ethical issues |
Case-control study |
Relatively small number of participants needed Disease objectively confirmed No follow-up period needed; no drop-outs |
Risk cannot be calculated Prone to selection bias, recall bias and confounding Limit to exposures studied Difficult to acquire biological samples |
Cohort studies
A cohort is a group of people followed over a period, some of whom will have the exposure of interest and some of whom will have the outcome of interest. Participants are assessed for many exposures in addition to that under investigation and often have biological samples taken. For rare exposures, it is necessary to find cohorts with a high prevalence of exposure, such as occupational groups (Kachuri et al, 2016), while general population cohorts are used for more common exposures (Riboli, 2001). A randomised trial can be thought of as a type of cohort study where the exposure is randomly assigned by the researcher. Field trials are the custom in cancer epidemiology, where participants in the community are randomised, either individually or by group (e.g. by area of residence or clinic attended).
The Gambia Hepatitis Intervention Study (The Gambia Hepatitis Study Group, 1987)
The Gambia Hepatitis Intervention Study is a large-scale study of the prevention of liver cancer by hepatitis B (HBV) vaccination of young infants. The latest estimates (Viviani et al, 2008) indicate that the number of cases needed to detect a significant difference between vaccinated and unvaccinated groups will be reached when subjects are around 30 years old, between 2017 and 2020.
Case-control studies
Case-control studies begin with identified cases of cancer whose exposures are compared to those of a group of people without cancer (controls). Both groups are drawn from the same source population. The source population may be patients attending a hospital or clinic, the population of a region or other defined population. The control group is chosen at random from this source population. Sometimes, cases and controls are drawn from an existing cohort. This would be a nested case-control study which provides better quality information on exposures.
Sources of Error in Risk Factor Studies
The errors which occur in studies of causation are of two kinds: systematic and random. Systematic error is unaffected by study size, while random error decreases with increasing study size.
Systematic error
Systematic errors are divided into bias and confounding.
- Bias can be considered as an error in the conduct of a study (selection bias, measurement bias)
- Confounding is an error in study design or interpretation of study results
Bias
Selection bias occurs when the exposed and unexposed populations differ in ways (other than the exposure) which affect the outcome. Selection bias can give rise to the ‘healthy worker’ effect, where the effect of an occupational exposure is countered by the overall better health of those in active work (Zielinski et al, 2009). Selection bias may also occur if participants volunteer for the study for reasons related to the exposure, e.g. interest in a healthy lifestyle. Bias is difficult to avoid in the selection of the controls for case-control studies. They may be chosen from patients with non-cancer conditions attending the same hospital or from people living in the same area or attending the same family doctor, and so may have risk factors in common with cases.
Exposure measurement: Bias in recall of self-reported exposures is common in case-control studies. Bias may be differential between cases and controls, as patients with cancer are more likely to recall a specific exposure, or it may be non-differential, due to under-reporting of factors such as alcohol and tobacco intake. Differential bias may lead to over- or under-estimation of the effect, but non-differential bias will always lead to under-estimation. Where possible, self-reported exposures should be independently validated.
Outcome measurement: Bias in outcome measurement is uncommon in cancer epidemiology, although cancer diagnoses may be missed in cohorts for which the follow-up is inefficient. Overdiagnosis, or earlier diagnosis, may occur in cohorts where the exposed participants are more intensively monitored.
Confounding
Confounding is a common source of error in interpretation. A confounder is something which affects the outcome but not the exposure of interest, and is correlated with the exposure. For instance, heavy drinkers tend to smoke, which means that high alcohol consumption is associated with, but does not cause, lung cancer. Smoking is therefore a confounder of the relationship between alcohol and lung cancer. Confounding occurs frequently in cancer studies, due to the large number of potential carcinogenic exposures. While bias can be minimised by adherence to good study design and practice, minimising confounding requires a thorough knowledge, measurement and analysis of potential exposures and is usually part of study analysis as well as design.
Random Error
The relation between exposure and outcome is unpredictable at the individual level, and measures of effect in individuals will be randomly distributed around some best estimate (e.g. an average). The usual measure for showing the scatter around the estimate is the 95% confidence interval. There are various interpretations of this interval, but in practice it is used to test if the data are consistent with some hypothesis. Random error reduces with study size but can also be reduced by study design and conduct and by having a homogeneous study population.
Statistical Testing
Statistical testing determines how consistent the measured effect is with a hypothesised effect. The hypothesis is usually that there is no effect, or that there is no difference between two effects (null hypothesis). Conventionally, if the 95% confidence intervals of the measured effect do not overlap those associated with the null hypothesis, it is considered that there is a real effect. Confidence intervals are more informative than probabilities (p-values) which give little information about the underlying data.Risk ratios and odds ratios are conventionally presented as unadjusted and adjusted. The unadjusted ratio is the simple risk ratio or odds ratio (risk exposed/risk unexposed). On the other hand, an adjusted ratio arises from statistical models which allow for the effects of other variables and confounders (e.g. age, sex, smoking, body mass index) which may affect the risk.
Table 4: Unadjusted and Adjusted Odds Ratios and 95% Confidence Intervals for Colorectal Cancer Risk Associated With Duration of Observed Insulin Exposure
Cases |
Controls |
Unadjusted odds ratio (95% confidence interval) |
Adjusted odds ratio (95% confidence interval)* |
|
|---|---|---|---|---|
No insulin therapy (reference) |
107 (83.6) |
1084 (87.5) |
1.0 |
1.0 |
≥5 years of insulin use |
4 (3.1) |
15 (1.2) |
2.8 (0.9–8.5) |
4.7 (1.3–16.7) |
*Adjusted for sex and 7 other variables. | ||||
From Yang YX, Hennessy S, Lewis JD. Insulin therapy and colorectal cancer risk among type 2 diabetes mellitus patients. Gastroenterology 2004; 127:1044-1050. Copyright © 2004. Reprinted with permission from the American Gastroenterological Association.
Interpretation
How important is the effect? Two factors determine the clinical importance of an effect:
- The size of the effect
- The frequency of occurrence of the exposure
Large effects, even with wide confidence intervals, should not be ignored if they fulfil criteria of plausibility. Small, statistically significant effects are common in large studies, but may be artefactual. However, small effects with high exposure prevalence may have public health importance. Where the background risk is low, risk difference is more informative than risk ratio, because the risk ratio may exaggerate the importance of an effect. The STROBE (Strengthening the Reporting of Observational Studies in Epidemiology) initiative has produced a detailed guide on the reporting and interpretation of observational studies (Vandenbroucke et al, 2007), which describes how these studies should be reported.
Representativeness
Studies of cancer risk factors are investigations of aetiology, which are presumed to have a biological basis. Although there may be differences in susceptibility between populations, the effects of risk factors are usually similar in all populations. Good study design is therefore more important (Doll et al, 2004) than the issue of whether the participants are representative of the wider population.
Publication Bias
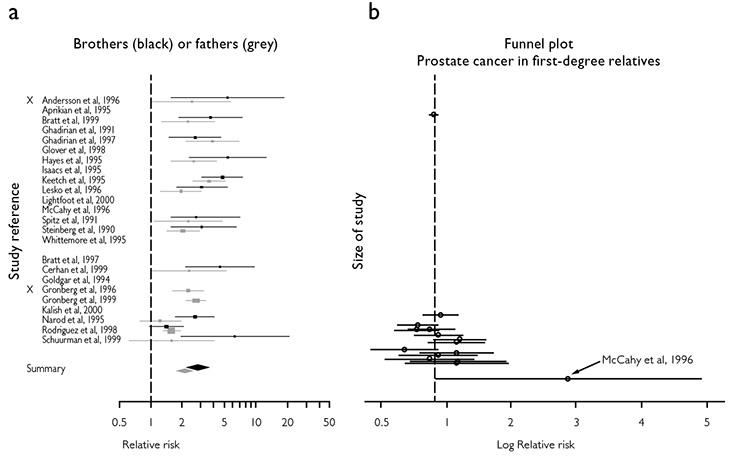
Many initial studies of risk are small and poorly designed. If they test a novel hypothesis, they are less likely to be published if they fail to support this hypothesis. If published, they are likely to be followed by larger studies, which are more likely to be published. Small negative studies of risk tend to be under-reported, leading to bias in reviews and meta-analysis. Figure 1(a) shows the forest plot of a meta-analysis of the risk of prostate cancer in first-degree relatives of prostate cancer patients (Bruner et al, 2003). In the same figure, (b) shows a funnel plot of the same data. The vertical dashed line indicates the weighted average, around which individual studies should be symmetrically grouped. The smaller studies (at the bottom) are skewed to the right, suggesting that smaller negative studies were less likely to be published, causing publication bias.
Figure 1: Relative Risks
(a) Relative risks of prostate cancer in men with a history of prostate cancer in a first-degree relative. (b) Funnel plot for first-degree relatives. The circles represent the estimates of the log relative risk for each study and the horizontal lines are 95% confidence intervals.
From Bruner DW, Moore D, Parlanti A, et al. Relative risk of prostate cancer for men with affected relatives: systematic review and meta-analysis. Int J Cancer 2003; 107:797-803. By permission of John Wiley and Sons.
Glossary
Adjusted ratio: The effect calculated following adjustment of the data to take account of variables or confounders that might have an impact on the effect. See also: Unadjusted ratio.
Bias: Distortion in the data that can lead to conclusions that are systematically incorrect.
Case-control studies: Observational study in which the effect of an exposure is measured by comparing the history of exposure between cases (individuals who have, or die of, the disease) and controls (individuals without, or who do not die of, the disease).
Cohort: Analytic study of a group (cohort) defined by exposure characteristics or a process of recruitment. Outcomes are ascertained and compared in all members of the cohort.
Confidence interval: A statistical measure of precision for an estimate of a population parameter. Various levels of confidence in the point estimate can be defined, but the 95% confidence interval is commonly used. The interval shows the range of values in which the true value of a parameter should occur 95 times out of 100 if the population of interest is sampled repeatedly.
Confounding: A source of error in interpretation which occurs when the effect of an exposure on an outcome is affected by another exposure, which is correlated with the first exposure.
Control group: Group of patients who receive usual care, which acts as the comparator for the group receiving the new intervention or the exposure.
Differential: Bias that arises in the reporting of factors (such as exposure to risk factors for cancer) between people that have and have not been diagnosed with the condition, because of their knowledge of the diagnosis.
Field trials: Clinical trial carried out in a community setting.
Follow-up: The monitoring of participants in a study for a period of time
Forest plot: A graphical representation of the data from a meta-analysis, showing a line of data for each included study and the overall estimate from combining the results of the individual studies.
Funnel plot: A graphical representation of effect estimates plotted against a measure of size or precision for individual studies pertaining to a research question. The resulting plot should have a symmetrical, triangular distribution in the absence of biases related to study size.
Hypotheses: Scientific statement that is postulated and can be investigated by means of empirical data.
Meta-analysis: Statistical combination of data from a series of studies (usually in a systematic review) to obtain one summary effect estimate. Results are often displayed in a forest plot.
Mortality: Deaths of participants in the trial, usually within a specified time period.
Nested case-control study: Case-control study in which both cases and controls are drawn from a pre-existing cohort study.
Non-differential: Bias that causes misclassification of exposure but which is not related to knowledge of the diagnosis of a condition.
Null hypothesis: The assumption that there is no true difference in the effects of the treatments being compared.
Observational study: A research study to measure the effect of an exposure/intervention by observing the participants in their natural setting.
p-values: Probability of getting the observed data or data deviating even more from the expected values if the null hypothesis is true.
Odds ratio: The ratio of the odds that an event occurred in one group (usually the intervention or exposure group) to the odds of the event in a second group (usually the control group).
Prevalence: Number of cases with a particular disease who are alive on a certain date.
Publication bias: Selective reporting of a research study based on its findings.
Random error: Error due to the inherent unpredictability of events or that are inherent in the difference between a sample and the whole population
Randomised trial: Study in which patients are allocated randomly to one of the groups being compared.
Selection bias: Bias in choosing the individuals or groups to take part in a study, which might make them systematically different from those who do not take part.
Source population: A hypothetical population from which the cases and controls in a case-control study are drawn.
Statistical testing: Statistical process to determine whether to reject or accept the null hypothesis based on the degree of the deviation of observed data from those expected if the null hypothesis is true.
Statistically significant: Result of a statistical test that rejects the null hypothesis based on the deviation of observed data from those expected if the null hypothesis is true.
STROBE: Strengthen the Reporting of Observational studies in Epidemiology: guidelines on reporting the results of observational studies.
Systematic error: Consistent error in either the study population or the information gathered, leading to a measured value which deviates from the true value.
Unadjusted ratio: The effect calculated simply from the data with no adjustment for any variables or confounders that might have an impact on the effect.